2几何光学成像

2.3半球面折射及透镜成像

半球面折射成像

阿贝不变式：
$$
\frac{n’}{s’} - \frac{n}{s} = \frac{n’ - n}{r}
$$
物方像方焦点公式：
$$
f = \frac{nr}{n - n’}\
f’ = \frac{n’r}{n’ - n}\
\frac{f}{f’} = -\frac{n}{n’}
$$

关于我对老师所教的一套符号法则的理解和总结：

用加号高斯公式时，所有距离全正（几何长度）
用减号折射/笛卡尔公式时，所有距离按方向带正负号
焦距符号永远物理推导

透镜成像相关公式

磨镜者公式：
$$

f = f’ = \frac{1}{(n_L - 1)\left( \frac{1}{r_1} - \frac{1}{r_2} \right)}
$$
透镜成像高斯公式（左为一般形式）：
$$
\frac{f’}{s’} + \frac{f}{s} = 1 \overset{f = f’}{\Rightarrow} \frac{1}{s’} + \frac{1}{s} = \frac{1}{f}
$$
右式用途广泛。

注意：

这两个公式所说的f是整个薄透镜的焦距而不是单个球面。凸透镜为正，凹透镜为负。

透镜成像牛顿公式：

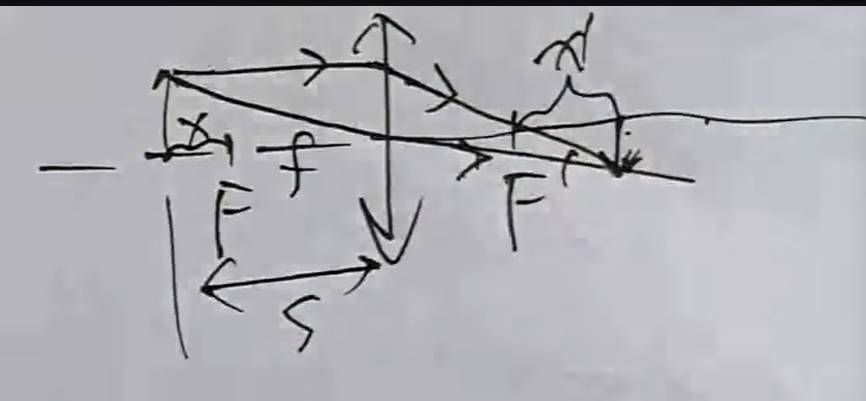
$$
\left{
\begin{aligned}
s &= x + f \
s’ &= x’ + f’
\end{aligned}
\right.
\overset{将这两个式子带入高斯公式得到}{\Rightarrow} xx’ = f^2
$$

主要探讨了物/像分别到焦点的距离x/x’和焦距f的关系。

两类薄透镜作图法（略）

重点讲解：作平行于入射光线的副光轴交焦平面于副焦点，把然后按照常规来做。

凸透镜：

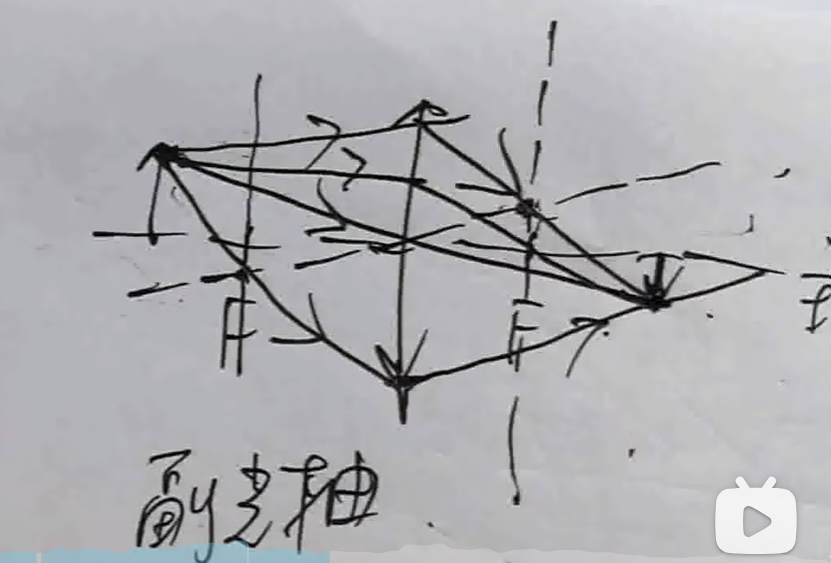
凹透镜：

球面反射

$$
f = \frac{r}{2}
$$
作图与以上一致。

放大率

重点只看两个，线放大率$\beta$ 和轴向放大率$\alpha$

线放大率$\beta$

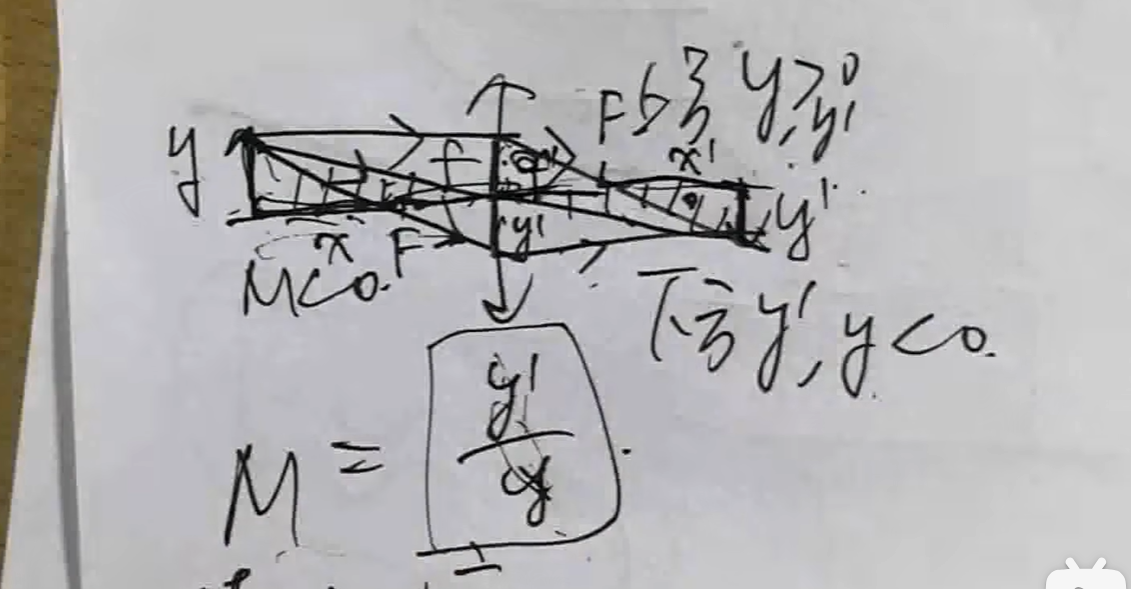
图中有另外两对相似三角形来表示它，左下，右上。

轴向放大率$\alpha$

2.4逐次成像法

$$
-f_1 = \frac{r_1}{1 - n}\
f_1’ = \frac{nr_1}{n - 1}\
f_2 = \frac{-nr_2}{n - 1}\
-f_2’ = \frac{-r_2}{1 - n}\
f = \frac{f_1f_2}{\Delta} \overset{带入f_1f_2以及\Delta =f_2 - f_1’ + d }{\Rightarrow} f = \frac{f_1f_2}{f_2 - f_1’ + d} \Rightarrow
$$